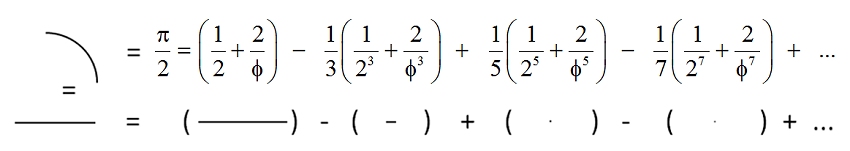|
Phi and Pi III - 2014 - 127cm x 78cm. Engraved and painted sandstone. [not for sale]
|
||
 |
||
|
|
||
 |
 |
|
|
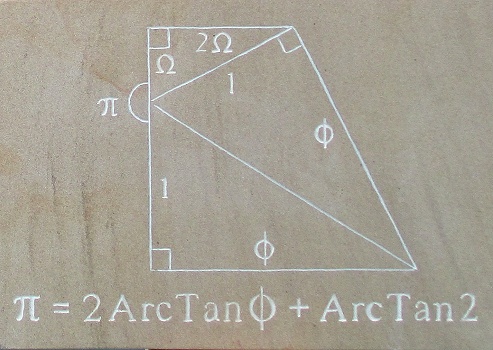
Phi and Pi I. 2014. 30cm x 30cm
Engraved and painted sandstone. |
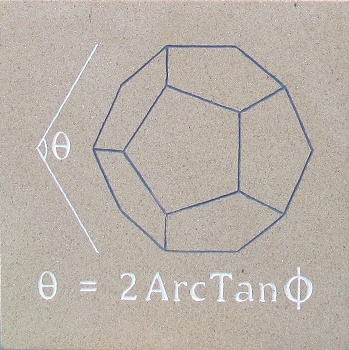
Phi and Pi II. 2014. 30cm x 42cm
Engraved and painted sandstone. |
|
|
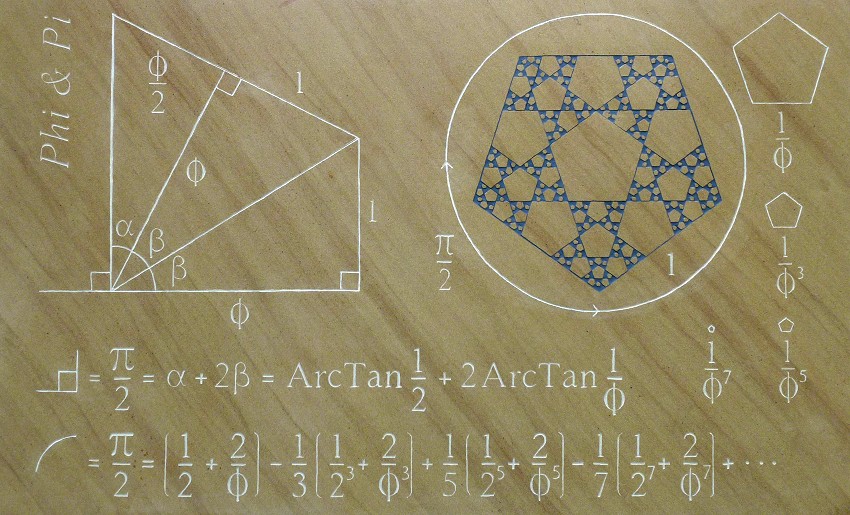
The edge lengths involved in the terms of the series for pi are the odd inverse powers - 1/Φ, 1/Φ3, 1/Φ5, 1/Φ7, etc.... 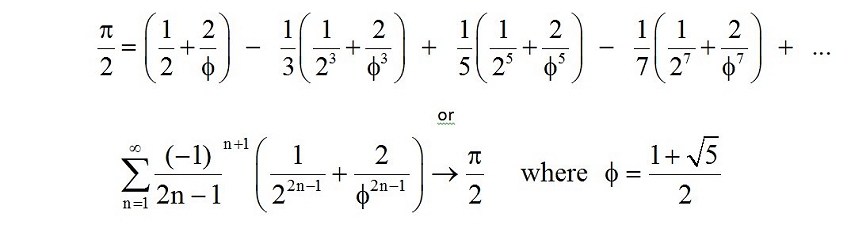
I rather like fractions and phi, but here are other versions, for those of you who don’t: 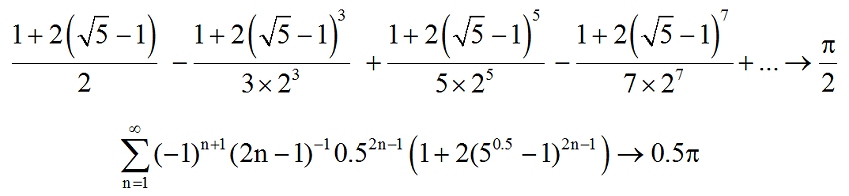
1 MILNER, J. 2002. The Dodecahedron, the Icosahedron and the Golden Section. Unpublished paper. Sheffield Hallam University, UK. |
||